About Ko in a Semeai Between
Two One-Eyed Groups (2012)
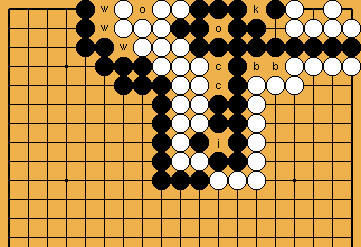
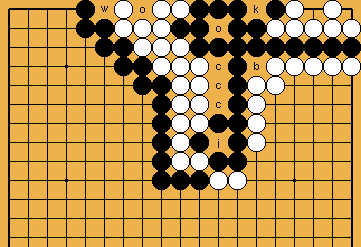
[ Shared Ko-Shape in the Centre ]
|
EX = 2: |
|
|
|
|
|
EX = 2 / -f: |
|
|
|
The number of Black's ko-threats needed to win - from here on - is t = ( |
|
EX = 2 / -c -f: |
|
The number of Black's ko-threats needed to win is t = ( Please note, that there will be no ko in the problem, due to the number of White's liberties. |
|
EX = 2 / -c -2f: The number of Black's ko-threats needed to win still is t = ( |
|
EX = 2 / -2f: The number of Black's ko-threats needed to win is t = ( This again highlights that White must think twice before filling in her second false eye, as well as Black must be careful not to occupy shared liberties too early (i.e. as long as there are still sufficient outside liberties available). |
Conclusion: Both basic shapes that are relevant for the problem - the larger eye for Black and the second ko-shape in the centre - show identical results, as far as the number of (exceeding) ko-threats in concerned, which Black needs to win the ko-fight. White must not fill in her second eye unforced. Black should not occupy shared liberties too early. With the larger eye, Black has an internal ko-threat (the capture of White's two stones), not available with the second ko-shape, so this shape might be preferable for Black. However, we will show later (please refer to | |
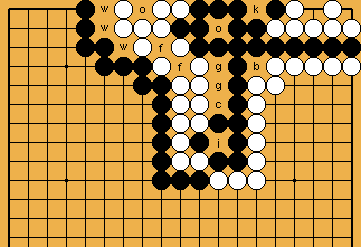
 ). In principle, the results will be the same, as far as questions of the ko are concerned.
). In principle, the results will be the same, as far as questions of the ko are concerned.
 :
: -points.
-points.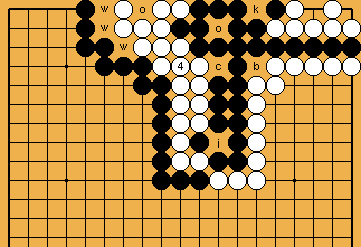
 :
: +
+  ) - 1 = 3 only. The
) - 1 = 3 only. The 
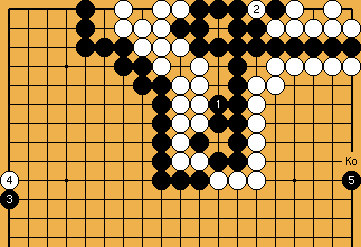
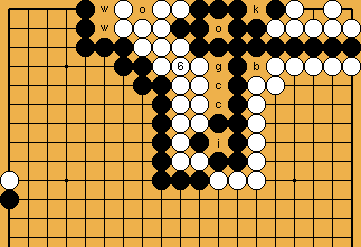
 :
: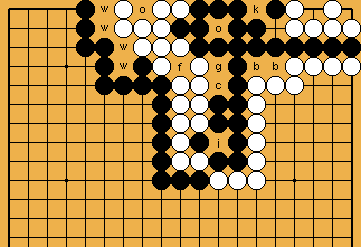
 -liberty and two White
-liberty and two White 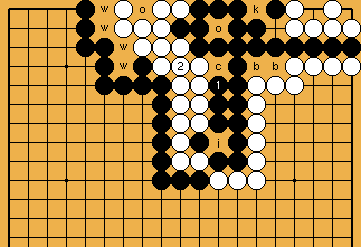
 1165
1165
