About Ko in a Semeai Between
Two One-Eyed Groups (2012)
The Simple Version - No Hanezeki
|
|
|
///:
|
|
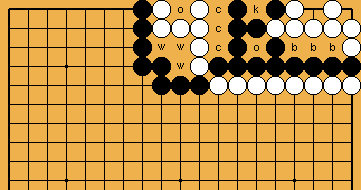
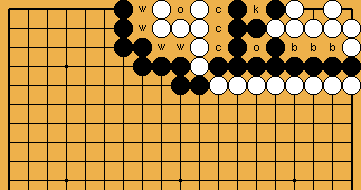
N. B.: We will display ko-threats (and their response) in the lower left part of the board; moves which capture the ko, in the lower right. Moves that are played in the top left corner, like |
|
///:
|
|
|
|
///:
|
|
From here on, we will distinguish several cases by the difference "EX" of White's liberties ( This position has EX = 1; Black needed one more ko-threat than White to make up for White's exceeding liberty. We will use the letter "t" to reference this amount of exceeding Black ko-threats; here, t = 1 = EX. |
|
///:
|
|
|
|
|
|
Please note a very important feature that is characteristic for this case EX = 1. White's group has only two liberties left ( In general, White's ko-threats must reduce a surrounding Black group to one liberty less than her group has at the moment. Otherwise, Black would simply take further liberties of her group, and win. |
|
|
|
///:
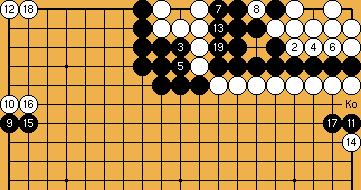
Taking the liberty in the ko has the same effect as taking any other liberty of Black's group, but the disadvantage of changing the parity (whose turn it is to take the ko) of the ko. So, White should keep this move until the very end. |
|
///: EX = 0 |
|
N. B.: We will not display this case "EX = 0" with the positions following below, because nothing extraordinary is supposed to happen herewith. |
|
///: EX = 2 |
|
|
|
///:
|
|
///:
|
|
///: EX = 3 |
|
t = 6 = ( N.B.: In the following, we will restrict ourselves to displaying the case "EX = 2" (as an example for "EX >= 2"), because all further cases "EX = 3, 4, ..." follow the same formula. |
Conclusion: EX = 0. Black will win unconditionally. In the problem, this case can only happen after two White mistakes. EX = 1. Black needs one more ko-threat than White. In the problem, Black has at least two ko-threats on the right side of the board, and all of White's ko-threats must be atari. In principle, Black will win this case, which can only happen after a White mistake, losing a move. EX >= 2. Black needs one ko-threat less than White has ko-fight liberties, counted at the moment, White starts the ko. Smaller EX are better for Black. | |
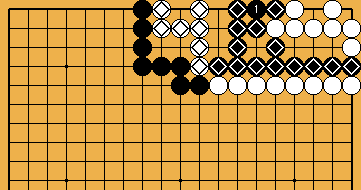
 :
: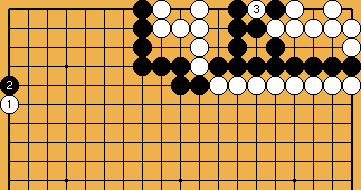
 :
: ,
,  ), and ...
), and ...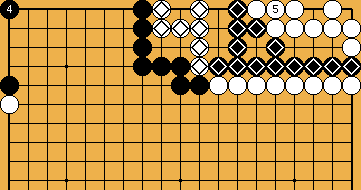
 :
: . Again, there is the seki between the two marked groups.
. Again, there is the seki between the two marked groups.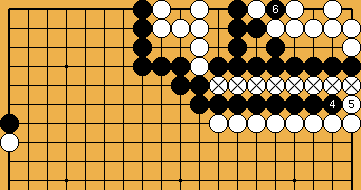
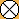 ), as here, with
), as here, with 
 :
: ) to take one liberty of White's group in the semeai, in return.
) to take one liberty of White's group in the semeai, in return.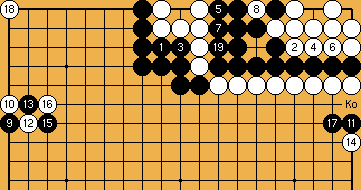
 ) more than White does.
) more than White does.
 +
+  ), and Black's liberties (
), and Black's liberties ( ), which is the amount of White's exceeding liberties: EX = (
), which is the amount of White's exceeding liberties: EX = (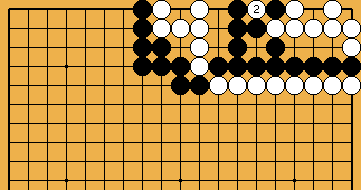
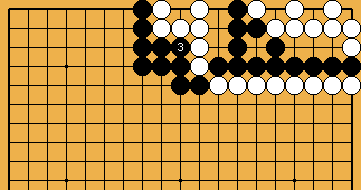
 :
:
 :
:
 :
:
 :
: would be an atari), so - in the problem - White's ko-threat must be an atari, too, on any of Black's surrounding groups.
would be an atari), so - in the problem - White's ko-threat must be an atari, too, on any of Black's surrounding groups.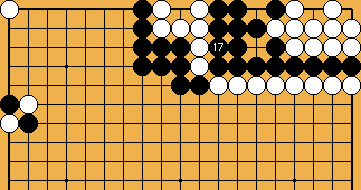
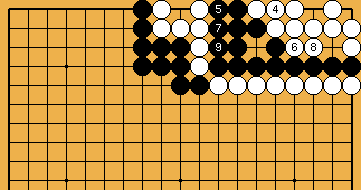
 :
:
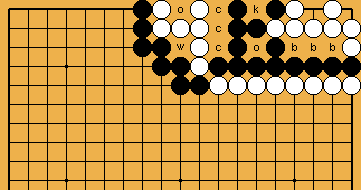
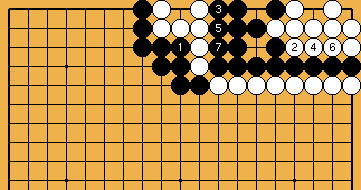
 :
:

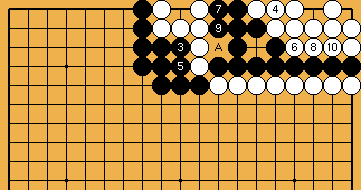
 .
.
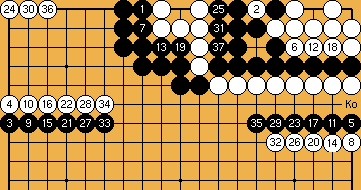
 :
:
