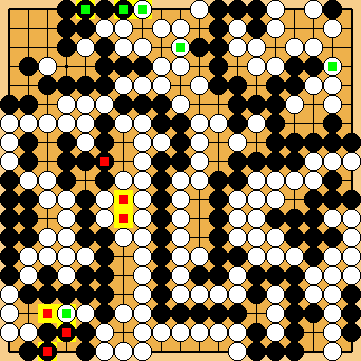
Variations of Our Solution (III)
VAR 

|
|
|
Connecting at
Playing the tesuji of
Connecting at |
|
|
|
Please note that Black has to capture White's large group in the Semeai Variation at the very end, due to the lack of eyes in his surrounding group in the centre. |
|
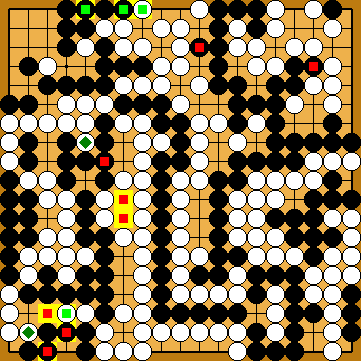
Capture Variation: Compared to the superordinate variation, ...
In total, gains and losses compensate for each other. White + 1 => White + 1 |
|
Semeai Variation: Compared to the superordinate variation, ...
In total, gains and losses compensate for each other. White + 1 => White + 1 |

 548k
548k
 :
: : (129
: (129  548kla
548kla would be too early and cost her one point (and so the win of the game).
would be too early and cost her one point (and so the win of the game). : (A
: (A  is possible and will not change the result of the game. But this move would worsen the Semeai Variation by one point.
is possible and will not change the result of the game. But this move would worsen the Semeai Variation by one point. : (B
: (B  in the lower left corner is also possible and will not change the result of the game. But this move would worsen the Semeai Variation by one point.
in the lower left corner is also possible and will not change the result of the game. But this move would worsen the Semeai Variation by one point.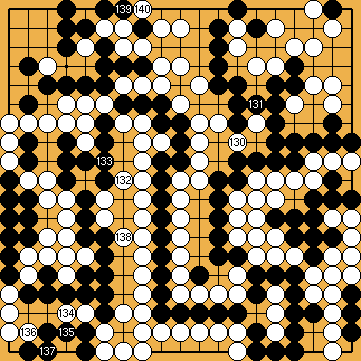
 :
: , so Black has to connect solidly.
, so Black has to connect solidly. ,
,  :
: :
: :
:
 :
: ,
,  ,
,  :
: