Variations of Our Solution (IIIa)
No Early Kikashi
VAR  (.3)
(.3)  (.1)
(.1)  (.1)
(.1) 

|
|
|
|
|
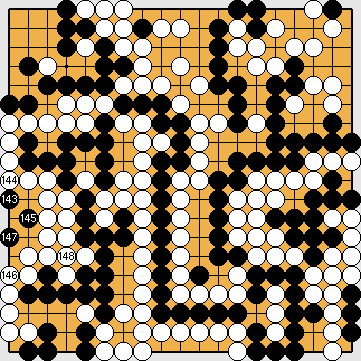
White will not choose Dany's Sacrifice here, as Black will win the game. |
|
Black plays 4/7 reductions. With 7/7 reductions, the final scores would be Black + 2 / White + 6. After Black occupied White's liberty at |
|
Capture Variation: Compared to the superordinate variation ...
In total, gains and losses compensate for each other. White + 1 => White + 1 |
|
Semeai Variation: At White's decision point, Black's large group in the upper right will have ten liberties, nine direct liberties ( Black will win the game by a large margin. |

 648jx
648jx
 ;
;  :
: :
:
 :
:
 , White will force him to capture her single stone in the left centre "early". Thereafter, she will play her kikashi
, White will force him to capture her single stone in the left centre "early". Thereafter, she will play her kikashi  ,
,  in the lower left corner, so that Black has to capture at
in the lower left corner, so that Black has to capture at  before the end of the game.
before the end of the game.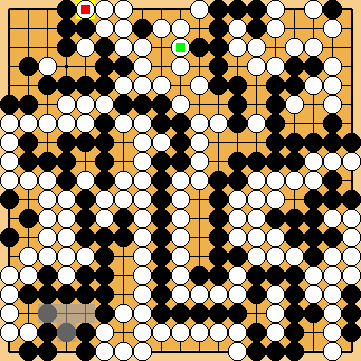

 ), and one approach-move liberty (
), and one approach-move liberty ( ), so White will be unable to capture it.
), so White will be unable to capture it.
