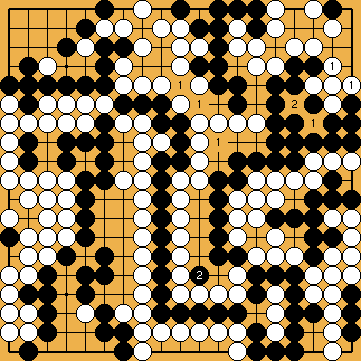
Variations of the Professional Solution
VARP 

|
(Referenced by
But by starting the ko on the left side, White may unnecessarily open a Pandora's box, because this ko-fight may become very complicated. We will explain just some of our thoughts, because this could be a surprising second chance for Black to win the game, after having missed the guzumi earlier. However, the opportunity for winning the game by playing the guzumi has closed with the completion of the Crosscut Sequence (please refer to the section "The Timing of the Guzumi"; |
|
|
|
|
|
|
|
|
|
|
|
White wins by four points. It is a very astonishing aspect of this problem that living with the group in the upper right without having the seki in the lover right quadrant of the board resolved does not profit Black. |
|
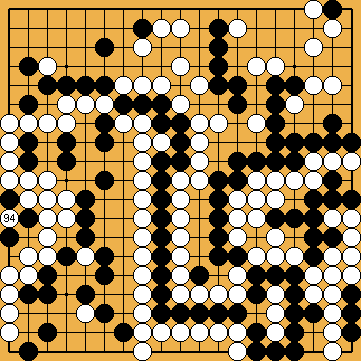
Let us first return to the result of the Capture Variation of our solution, where Black also played the guzumi, and compare it to the flow of this sub-variation. By further capturing in the nakade on the left side White gains an additional 3 + 4 = 7 prisoners ( In the centre, White captures 20 Black stones ( On the right side, Black gets 64 points by capturing 32 White stones ( In the lower right corner, each side captured a further four stones, which cancels each other out. So Black gets a surplus of 64 - 38 - 7 = 19 points. Seen the other way round, this means that Black is behind by 19 points in this sub-variation at the moment, he decided to try to live in the upper right. |
|
You will recognize that the gains and losses of the endgame on the left side of the board (compared to our solution) compensate for each other. In the other parts of the board, seen from Black's point of view, there is a gain of five points in the centre (3 * 1, 2), and a gain of a further five points in the upper right (3 * 1, 2), because White did not have her sente sequence available here, to close the borders like in the path of our solution. However - Black wins the Capture Variation of our solution by five points - a gain of only ten points is not sufficient to make up for the initial 19-points-disadvantage. As demonstrated above, White wins by four points. |
 822
822 731
731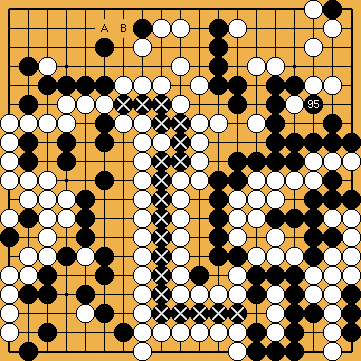
 :
: ). Now, the outcome depends on the upper left corner, i.e. on the point
). Now, the outcome depends on the upper left corner, i.e. on the point  for White, and the point
for White, and the point  for Black.
for Black.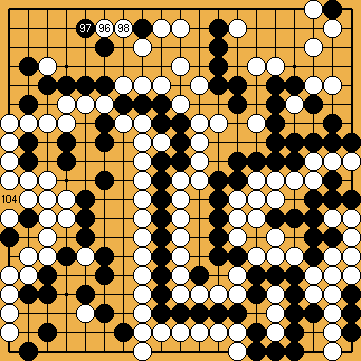
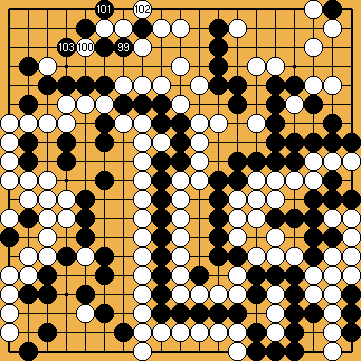
 : (104
: (104  735
735 .
.
 : (A
: (A 

 :
:
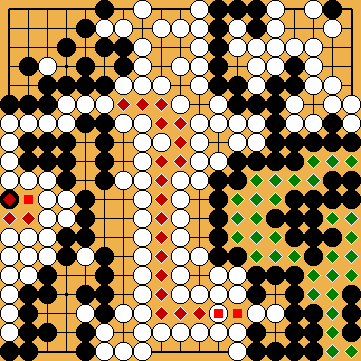
 /
/  /
/  ).
). ), to get 38 points of territory.
), to get 38 points of territory. ).
).